De la pratique du placebo chez l'idiophile, saison 4
Le coton-tige haut de gamme moderne est en fibres de carbone spécifications aviation (légèreté et solidité). Les cotons sont en pure laine vierge traitée multi-fibres qui associent de la laine Pashmelba pour la finesse du son et de la laine Shetlouf pour l'efficacité du nettoyage. La méthode d'enroulement choisie pour l'association des diverses laines dont chaque fibre calibrée n'excède pas l'épaisseur d'un cheveu, est celle qui prévaut dans les transformateurs toriques.
La difficulté de fabrication réside dans le collage subtil de la tige en carbone avec la boulette de laine. Ce collage est effectué à chaud, 55 °C, température supérieure à la température du corps pour ne pas risquer un décollement lors de l'utilisation. La colle utilisée est naturelle (poisson) d'où une légère odeur fétide mais sans danger pour les oreilles ni pour l'écoute ou pour les fusibles de l'amplificateur. Les boulettes de laine sont appairées pour garantir un nettoyage rigoureusement symétrique des oreilles de l'audiogogophile. Chaque unité de deux est testée en usine par un Coréen aux oreilles propres, le Coréen ayant une sensibilité très prononcée du conduit auditif. Le carbone, par sa légèreté et sa flexibilité permet un nettoyage sans risque mais très fin des oreilles.
Le prix est certes élevé, mais la différence de gain d'écoute entre un meilleur câble et un meilleur coton-tige est tellement en faveur de ce dernier que cela balaie toute hésitation.
À l'écoute, les basses sont plus nettes et les aiguës les plus élevées deviennent audibles sans aucune agressivité. Au contraire, elles retrouvent un soyeux que l'on avait oublié depuis l’abandon du cornet de téléphone. Les voix sont plus pures, le grain apparaît mieux alors que les applaudissements et toux cacochymes des salles de concert redeviennent d'un naturel saisissant. Tout dans ces cotons-tiges est au service de la musique. Nulle dureté du son, rien de forcé, tout redevient naturel. Bonne écoute.
Infos pratiques :
Livrés en boîtes de 2x12 sous vide et emballés individuellement.
À conserver au frigo à 6 °C et n'enlever du frigo qu'une demi-journée avant utilisation.
Respecter une période de rodage.
En changer avant chaque nouvelle écoute de CD.
Prix : 150 € par boîte pour le modèle premium et 1200 € pour la version Gold.
À consommer dans les limites des dates de péremption.
Ne pas utiliser pour écouter de la musique techno, metal ou rock.
Ça vous semble loufoque ? Eh bien allez donc lire les tests du magazine Diapason sur la Hi-Fi et ses accessoires et dites-moi ce que vous en pensez…
(source)
Derniers raffinements
Je vois que personne n'a vu l'erreur signalée dans le dernier article. Le problème était simple, il fallait réinitialiser le compteur lors de la transition extinction vers HT. En effet, l'état extinction impose la présence de la basse tension, mais la haute tension est coupée. Lorsque cette haute tension est rallumée, son temps de montée n'est pas nul. Il faut donc passer par l'état HT qui ne vérifie pas la présence de la haute tension avant de passer en défaut ou en maintien. Or la transition depuis extinction vers HT se fait avec un compteur dans un état indéfini alors que l'arrivée à l'état HT suppose un compteur nul.
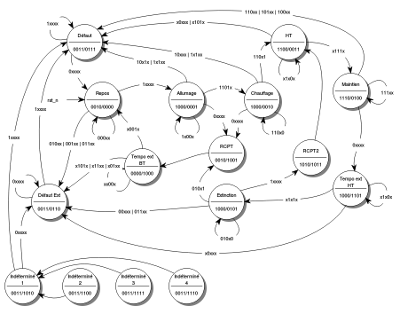
Fig. 1 : la même chose en grand
Les quatre états au bas du schéma sont des états normalement inaccessibles. Ils ont été rajoutés pour que tous les états soient déterminés et que le système passe en protection en cas de présence d'un état indéterminé.
Les nouvelles sorties de la machine sont maintenant :
| B | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | ||
| 11 | 1 | |||
| 10 | 1 | |||
Tab. 1 : allumage de la basse tension
B=Q3'(Q2'(Q0+Q1)+Q2Q1')+Q0(Q1 xor Q2)
| H | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | |||
| 11 | ||||
| 10 | ||||
Tab. 2 : allumage de la haute tension
H=Q3'(Q2Q1'Q0'+Q2'Q1Q0)
| R | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 | 1 | |
Tab. 3 : blocage du compteur à zéro
R=Q1(Q2+Q3)+Q3'Q1'Q0'+Q3(Q2 xor Q0)
| E | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | ||||
| 01 | 1 | 1 | ||
| 11 | 1 | 1 | 1 | |
| 10 | 1 | |||
Tab. 4 : indicateur d'erreur
E=Q2Q1+Q3Q0'(Q2+Q1)
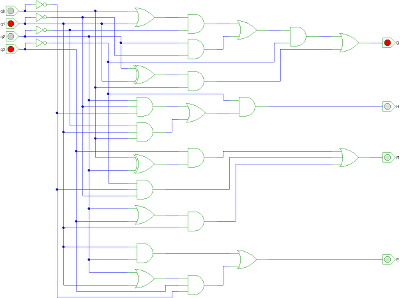
Fig. 2 : circuit de sortie de la machine (en grand)
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | 0 | 0 | 0 | 1 | X | X | X | X | ||||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | ||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | X | X | ||||||
| 0 | 0 | 1 | 0 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 1 | 0 | 1 | 1 | 1 | X | X | 1 | 1 | X | X | 0 |
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
| 1 | 0 | 1 | 1 | X | X | X | X | X | 0 | 0 | 1 | 1 | X | 1 | 0 | X | X | 0 | X | 0 |
| 1 | 0 | 1 | 0 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | X | 0 | 0 | X |
| 1 | 0 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | 1 | X | X | 0 | 1 | X |
| 1 | 1 | 0 | 0 | X | X | X | X | X | 1 | 0 | 1 | 0 | X | 0 | X | 1 | 1 | X | 0 | X |
| 1 | 1 | 1 | 1 | X | X | X | X | X | 1 | 0 | 1 | 0 | X | 0 | X | 1 | X | 0 | X | 1 |
| 1 | 1 | 1 | 0 | X | X | X | X | X | 1 | 0 | 1 | 0 | X | 0 | X | 1 | X | 0 | 0 | X |
Tab. 5 : transitions de l'automate
La réduction des quines et le schéma de câblage suivront au prochain épisode. Après tout, nous sommes dimanche.
Un pas de plus vers l'automatisation
Pour automatiser la réductions des quines, le programme présenté il y a quelques articles est modifié pour générer automatiquement les diverses équations réduites directement du tableau des transitions. La procédure se fait grâce à un premier programme qui transforme le tableau des transitions en autant de fichiers qu'il y a de commandes de bascules :
#!/usr/local/bin/rpl -csp
/*
* Format du fichier d'entrée :
* abcdefghia'b'c'd'j3k3j2k2j1k1j0k0
*/
TRANSITIONS
<<
{ "length*(1)" }
{ { "name" "transitions.global" } "sequential" "old"
"readonly" "flow" }
open format
0
-> F_IN NB_LIGNES
<<
while
F_IN "end of file" inquire not
repeat
""
do
F_IN read 1 get
until
if
dup "\n" same
F_IN "end of file" inquire or
then
drop true
else
+
false
end
end
if
dup "" same not
then
'NB_LIGNES' incr
else
drop
end
end
F_IN close
NB_LIGNES ->table
>>
14
-> L I
<<
{ "j3" "k3" "j2" "k2" "j1" "k1" "j0" "k0" }
forall E
{ "length*(*)" }
"name" "transitions." E +
if
dup "existence" inquire
then
{ "sequential" "replace" "readwrite" "flow" }
else
{ "sequential" "new" "readwrite" "flow" }
end
rot rot 2 ->list 1 ->list swap +
open format
-> FICHIER
<<
1 L size for K
L K 1 ->list get I dup sub
-> F
<<
if
F "0" same not
then
if
F "X" same
then
"*"
else
""
end
L K 1 ->list get 1 9 sub + "\n" +
1 ->list
FICHIER write
end
>>
next
FICHIER close
>>
'I' incr
next
>>
>>
Cette première étape est suivie par une seconde qui transforme l'écriture réduite des états en un fichier compréhensible par qmc-cli :
#!/usr/local/bin/rpl -csp
/*
* Format du fichier d'entrée :
* 010X00X
* *1111111
* *X000X01
*
* Le X correspond à une valeur indifférente. Les entiers binaires
* spécifiés doivent donner une combinaison vraie. Les lignes commençant par
* une étoile indiquent un résultat indifférent.
*/
PRINCIPAL
<<
{ "j0" "k0" "j1" "k1" "j2" "k2" "j3" "k3" }
forall I
I TRANSITIONS
next
>>
TRANSITIONS
<<
-> E
<<
{ "length*(1)" }
"name" "transitions." E + 2 ->list 1 ->list
{ "sequential" "old" "readonly" "flow" } +
open format
0
-> F_IN NB_LIGNES
<<
while
F_IN "end of file" inquire not
repeat
""
do
F_IN read 1 get
until
if
dup "\n" same
F_IN "end of file" inquire or
then
drop true
else
+
false
end
end
if
dup "" same not
then
'NB_LIGNES' incr
else
drop
end
end
F_IN close
NB_LIGNES ->list
>>
1
-> LISTE I
<<
do
LISTE I get ucase
-> E
<<
if
E "X" pos dup
then
// Il y a au moins un X
-> P
<<
{ "0" "1" } forall J
if
P 1 same
then
J E 2 over size sub +
elseif
P E size same
then
E 1 over size 1 - sub J +
else
E 1 P decr sub J +
E P incr E size sub +
end
next
LISTE swap I swap put swap
1 ->list + 'LISTE' sto
>>
else
// Pas de X, on passe au suivant
drop
'I' incr
end
>>
until
LISTE size I same
end
LISTE l->t << < >> sort
{ "length*(*)" }
"name" E ".in" +
if
dup "existence" inquire
then
{ "sequential" "replace" "flow" }
else
{ "sequential" "new" "flow" }
end
rot rot 2 ->list 1 ->list swap +
open format
-> F_OUT
<<
forall I
if
I "*" pos
then
"x" "# " I 2 over size sub + "b" + str->
b->r ->str +
else
"# " I + "b" + str-> b->r ->str
end
->str "\n" + 1 ->list F_OUT write
next
F_OUT close
>>
>>
>>
>>
À la fin de la procédure, les huit fichiers j0.in, j1.in, j2.in, j3.in, k0.in, k1.in, k2.in et k3.in sont créés. Reste à les faire passer dans la moulinette qmc-cli pour obtenir la réduction des quines.
Après réduction, les équations deviennent :
j0=q3'q2'((q1 xor i) + iC255)+q3'q2(q1'i'+iPHT)+q3'i(PBT'+q1PHT)
k0=q2'PBTC15(q1'iPHT'+q3'q1PHT)+q3'q2i'(q1+PHT)+q3q1'(q2'+q0PBT')
+q3'q2i'PBT'
j1=q3'q2'q0'i'(PBT+PHT)+q3'q0i(PHT+C15)+q3'q2(i(PBT'+PHT')+q0PHT)
+q3q2'q1'q0'(PHT+PBTC15)+q2q1'q0PBT'
k1=q3'q2'(q1'i'+q0PBTPHTC15)+q3'q2q0i'
j2=q3'q1'(q0'i'(PBT+PHT)+q0iPHT)+q3'q1(i(PBT'+qo'PHT)
+q0(PBT'+C15))+q3q2'q1'q0'(PHT+PBTC15)+q3'q0iPBT'C15
k2=q3'q0(q1'(i+PBTPHT'C255)+q1i')
j3=q3'q0'i'(q1 xor q2)+q1'i'(q3'q2PBTPHT'C255+q2'q0)
k3=q2'q1'q0'(PHT+C15)+q2q1'q0(PBT'+C15)
Le schéma du circuit de contrôle des alimentations devient alors :
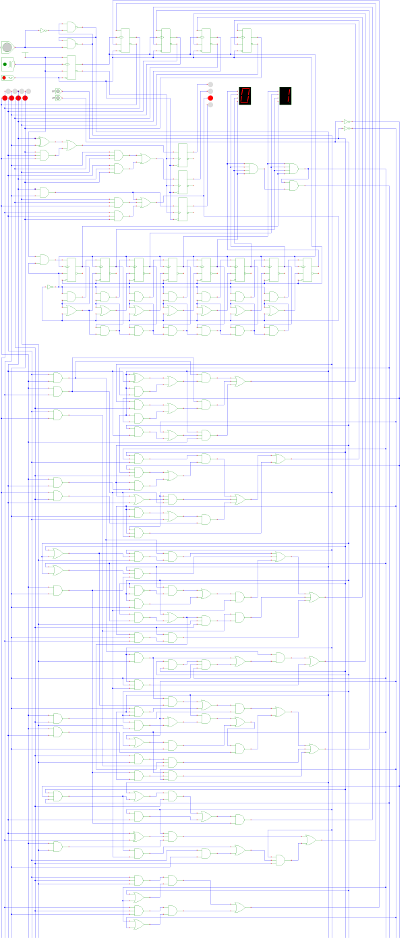
Fig. 1 : schéma de la machine à états (le même en grand)
J'ai pu tester ce circuit dans tous les sens. Il donne presque entièrement satisfaction. Tous les défauts sont bien détectés, les temporisations sont correctes pour les phases d'allumage et d'extinction. Ami lecteur, sauras-tu corriger ce circuit pour qu'il soit parfait ?
Et une erreur de plus, une !
Il y a toujours une erreur de plus. Confiant, j'avais simplifié les quines et câblé le circuit. Tout fonctionnait normalement jusqu'au test de réallumage de la haute tension depuis la procédure d'extinction. Là, le circuit que j'avais câblé se met en défaut car l'état 4 (haute tension avec test de la présence de la haute tension) suit l'état 5 (haute tension coupée, tension de chauffage présente).
Le fonctionnement est pourtant celui du graphe. En effet, il faut laisser à la haute tension le temps de s'établir avant que le circuit puisse tester sa présence. En cas de réallumage, l'état 3, et non le 4, doit suivre le 5. Voici doncle graphe modifié :
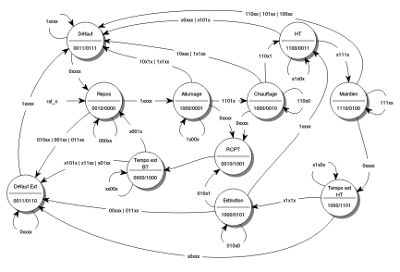
Fig. 1 : dernière version de l'automate (la même chose en grand)
La nouvelle table de transition — et j'espère la dernière — est la suivante :
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | 0 | 0 | 0 | 1 | X | X | X | X | ||||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | ||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | X | X | ||||||
| 0 | 0 | 1 | 0 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 0 | 0 | 1 | 1 | 0 | X | X | 1 | 1 | X | X | 0 |
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
Tab. 1 : transitions de l'automate
Ajout à l'automate d'une surveillance de la haute tension
Lors de la phase d'allumage, l'automate ne surveillait pas l'absence de haute tension (états 1 et 2). Ce nouvel automate vérifie ce point et indique une erreur en cas de présence de haute tension.
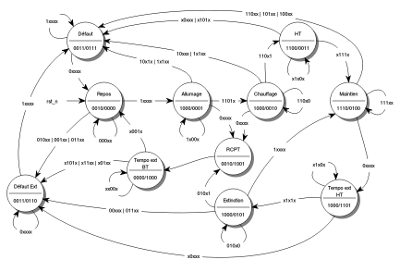
Fig. 1 : dernière version de l'automate (la même chose en grand)
La nouvelle table de transition est la suivante :
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | 0 | 0 | 0 | 1 | X | X | X | X | ||||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | ||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | X | X | ||||||
| 0 | 0 | 1 | 0 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 0 | 0 | X | X | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
Tab. 2 : transitions de l'automate