Catégorie: "Général"
Deprecated: Creation of dynamic property FiletypeCache::$mimetype_cache is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/files/model/_filetypecache.class.php on line 71
Deprecated: Creation of dynamic property calendar_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property calendar_plugin::$dbtable is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 53
Deprecated: Creation of dynamic property calendar_plugin::$dbprefix is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 54
Deprecated: Creation of dynamic property calendar_plugin::$dbIDname is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 55
Deprecated: Creation of dynamic property Calendar::$dbtable is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 508
Deprecated: Creation of dynamic property Calendar::$dbprefix is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 509
Deprecated: Creation of dynamic property Calendar::$dbIDname is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 510
Deprecated: Creation of dynamic property ItemQuery::$dbtablename is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 78
Deprecated: Creation of dynamic property ItemQuery::$dbprefix is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 79
Deprecated: Creation of dynamic property ItemQuery::$dbIDname is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 80
Deprecated: Creation of dynamic property Calendar::$ItemQuery is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 518
Deprecated: Creation of dynamic property Calendar::$linkpostcellstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 589
Deprecated: Creation of dynamic property Calendar::$linkposttodaycellstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 590
Deprecated: Creation of dynamic property Calendar::$todaycellstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 591
Deprecated: Creation of dynamic property Calendar::$todaycellstartpost is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 592
Deprecated: Creation of dynamic property Calendar::$postcount_month_atitle is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 606
Deprecated: Creation of dynamic property Calendar::$postcount_month_atitle_one is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 607
Deprecated: Creation of dynamic property Calendar::$postcount_year_atitle is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 608
Deprecated: Creation of dynamic property Calendar::$postcount_year_atitle_one is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_calendar.plugin.php on line 609
Deprecated: Creation of dynamic property Form::$form_name is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 146
Deprecated: Creation of dynamic property Form::$form_action is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 147
Deprecated: Creation of dynamic property Form::$form_method is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 148
Deprecated: Creation of dynamic property Form::$enctype is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 149
Deprecated: Creation of dynamic property Form::$layout is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 279
Deprecated: Creation of dynamic property Form::$template is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 283
Deprecated: Creation of dynamic property Form::$formclass is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 284
Deprecated: Creation of dynamic property Form::$formstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 285
Deprecated: Creation of dynamic property Form::$title_fmt is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 286
Deprecated: Creation of dynamic property Form::$no_title_fmt is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 287
Deprecated: Creation of dynamic property Form::$no_title_no_icons_fmt is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 288
Deprecated: Creation of dynamic property Form::$group_begin is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 289
Deprecated: Creation of dynamic property Form::$group_end is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 290
Deprecated: Creation of dynamic property Form::$fieldset_title is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 291
Deprecated: Creation of dynamic property Form::$fieldset_begin is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 292
Deprecated: Creation of dynamic property Form::$fieldset_end is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 293
Deprecated: Creation of dynamic property Form::$fieldstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 294
Deprecated: Creation of dynamic property Form::$labelclass is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 295
Deprecated: Creation of dynamic property Form::$labelstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 296
Deprecated: Creation of dynamic property Form::$labelend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 297
Deprecated: Creation of dynamic property Form::$labelempty is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 298
Deprecated: Creation of dynamic property Form::$inputstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 299
Deprecated: Creation of dynamic property Form::$inputend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 300
Deprecated: Creation of dynamic property Form::$infostart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 301
Deprecated: Creation of dynamic property Form::$infoend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 302
Deprecated: Creation of dynamic property Form::$fieldend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 303
Deprecated: Creation of dynamic property Form::$buttonsstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 304
Deprecated: Creation of dynamic property Form::$buttonsend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 305
Deprecated: Creation of dynamic property Form::$customstart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 306
Deprecated: Creation of dynamic property Form::$customend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 307
Deprecated: Creation of dynamic property Form::$note_format is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 308
Deprecated: Creation of dynamic property Form::$bottom_note_format is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 309
Deprecated: Creation of dynamic property Form::$formend is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 310
Deprecated: Creation of dynamic property Form::$fieldstart_checkbox is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 336
Deprecated: Creation of dynamic property Form::$fieldend_checkbox is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 337
Deprecated: Creation of dynamic property Form::$inputclass_checkbox is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 338
Deprecated: Creation of dynamic property Form::$inputstart_checkbox is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 339
Deprecated: Creation of dynamic property Form::$inputend_checkbox is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 340
Deprecated: Creation of dynamic property Form::$checkbox_newline_start is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 341
Deprecated: Creation of dynamic property Form::$checkbox_newline_end is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 342
Deprecated: Creation of dynamic property Form::$checkbox_basic_start is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 343
Deprecated: Creation of dynamic property Form::$checkbox_basic_end is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 344
Deprecated: Creation of dynamic property Form::$fieldstart_radio is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 346
Deprecated: Creation of dynamic property Form::$fieldend_radio is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 347
Deprecated: Creation of dynamic property Form::$inputclass_radio is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 348
Deprecated: Creation of dynamic property Form::$inputstart_radio is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 349
Deprecated: Creation of dynamic property Form::$inputend_radio is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 350
Deprecated: Creation of dynamic property Form::$radio_label_format is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 351
Deprecated: Creation of dynamic property Form::$radio_newline_start is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 352
Deprecated: Creation of dynamic property Form::$radio_newline_end is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 353
Deprecated: Creation of dynamic property Form::$radio_oneline_start is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 354
Deprecated: Creation of dynamic property Form::$radio_oneline_end is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/ui/forms/_form.class.php on line 355
Deprecated: Creation of dynamic property coll_category_list_Widget::$excluded_cat_IDs is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/widgets/widgets/_coll_category_list.widget.php on line 236
Deprecated: Creation of dynamic property ItemQuery::$dbtablename is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 78
Deprecated: Creation of dynamic property ItemQuery::$dbprefix is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 79
Deprecated: Creation of dynamic property ItemQuery::$dbIDname is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 80
Deprecated: strpos(): Passing null to parameter #1 ($haystack) of type string is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemquery.class.php on line 1418
Deprecated: Creation of dynamic property ItemLight::$objtype is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemlight.class.php on line 164
Deprecated: Creation of dynamic property ItemLight::$datestart is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_itemlight.class.php on line 175
Deprecated: Creation of dynamic property FiletypeCache::$mimetype_cache is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/files/model/_filetypecache.class.php on line 71
Deprecated: strtotime(): Passing null to parameter #1 ($datetime) of type string is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/files/model/_file.class.php on line 1015
Random photo
 |
Ajout à l'automate d'une surveillance de la haute tension
Deprecated: Creation of dynamic property Item::$cache_has_content_parts is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 4911
Deprecated: Creation of dynamic property smilies_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property quicktags_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property archives_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property archives_plugin::$dbtable is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_archives.plugin.php on line 54
Deprecated: Creation of dynamic property archives_plugin::$dbprefix is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_archives.plugin.php on line 55
Deprecated: Creation of dynamic property archives_plugin::$dbIDname is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/plugins/_archives.plugin.php on line 56
Deprecated: Creation of dynamic property email_elements_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property financial_contribution_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property ping_b2evonet_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property ping_pingomatic_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property auto_p_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property texturize_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property nofollow_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property content_blocks_plugin::$classfile_path is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/plugins/model/_plugins.class.php on line 413
Deprecated: Creation of dynamic property Item::$renderers_validated is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 11107
Deprecated: Creation of dynamic property Item::$pages is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 2412
Deprecated: Creation of dynamic property ItemSettings::$count_col_key_names is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/settings/model/_abstractsettings.class.php on line 121
Lors de la phase d'allumage, l'automate ne surveillait pas l'absence de haute tension (états 1 et 2). Ce nouvel automate vérifie ce point et indique une erreur en cas de présence de haute tension.
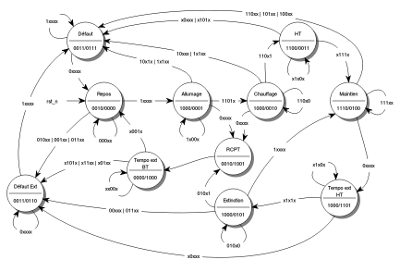
Fig. 1 : dernière version de l'automate (la même chose en grand)
La nouvelle table de transition est la suivante :
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | 0 | 0 | 0 | 1 | X | X | X | X | ||||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | ||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | X | X | ||||||
| 0 | 0 | 1 | 0 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 0 | 0 | X | X | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
Tab. 2 : transitions de l'automate
Automate, suite
Deprecated: Creation of dynamic property Item::$cache_has_content_parts is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 4911
Deprecated: Creation of dynamic property Item::$renderers_validated is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 11107
Deprecated: Creation of dynamic property Item::$pages is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 2412
Deprecated: Creation of dynamic property ItemSettings::$count_col_key_names is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/settings/model/_abstractsettings.class.php on line 121
Comme il faut toujours remettre son ouvrage sur le travail, voici la dernière version de l'automate à états finis gérant l'alimentation.
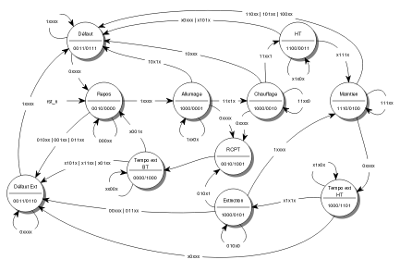
Fig. 1 : dernière version de l'automate (la même chose en grand)
J'espère cette fois-ci n'avoir rien oublié. Ce nouvel automate comporte onze états, donc nécessite quatre bascules au lieu de trois. Il faut donc réétudier les sorties du circuit à l'aide de nouveaux tableaux de Karnaugh.
| B | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | ||
| 11 | X | 1 | X | X |
| 10 | X | X | ||
Tab. 1 : allumage de la basse tension
B=Q1'Q2+Q0Q2'Q3'+Q1Q2'
| H | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | |||
| 11 | X | X | X | |
| 10 | X | X | ||
Tab. 2 : allumage de la haute tension
H=Q2Q1'Q0'+Q2'Q1Q0
| R | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | 1 | 1 | |
| 11 | X | X | X | |
| 10 | 1 | X | X | |
Tab. 3 : blocage du compteur à zéro
R=Q3'Q1'Q0'+Q3Q2'Q0+Q2Q1
| E | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | ||||
| 01 | 1 | 1 | ||
| 11 | X | X | X | |
| 10 | X | X | ||
Tab. 4 : indicateur d'erreur
E=Q2Q1
Le schéma des quatre sorties devient alors :
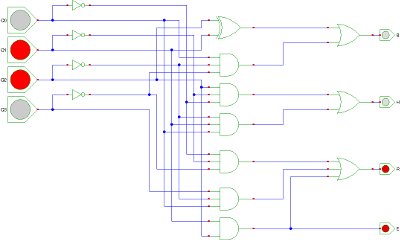
Fig. 1 : câblage des sorties (la même chose en grand)
Reste à écrire la table des transitions et à simplifier les quines.
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | X | 0 | 0 | 0 | 1 | X | X | X | X | |||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | X | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | ||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | X | 0 | 0 | 1 | 0 | X | X | X | X | |||||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 0 | 0 | X | X | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
Tab. 2 : transitions de l'automate
Simplification des quines
Deprecated: Creation of dynamic property Item::$cache_has_content_parts is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 4911
Deprecated: Creation of dynamic property Item::$renderers_validated is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 11107
Deprecated: Creation of dynamic property Item::$pages is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 2412
Deprecated: Creation of dynamic property ItemSettings::$count_col_key_names is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/settings/model/_abstractsettings.class.php on line 121
N'ayant pas encore d'hypercube à ma disposition pour écrire des tableaux de Karnaugh à plus de six variables, il convient d'utiliser les techniques de réduction de Mc Cluskey. Je vous fais grâce des calculs. Pour des raisons de simplicité d'écriture, les apostrophes notent une condition inversée. En voici les résultats :
J2=Q1'Q0'I'PHT+Q1'Q0'I'PBT+Q0IPBT'C15+Q1IPBT'+Q1Q0PBT'+Q1Q0C15
K2=Q0I'PBTPHT'C255+Q1Q0I'
J1=Q2'Q0'I'PHT+Q2'Q0'I'PBT+Q2'Q0IC15+Q2Q0'IPBT'+Q2Q0'IPHT'
+Q2Q0I'PBT'+Q2Q0I'PHT
K1=Q2'Q0'I'+Q2'Q0PBTPHTC15+Q2Q0I'
J0=Q2'Q1'I+IPBT'+Q2Q1'I'+Q2Q1I+Q1'IPHT'+Q2'IC255
K0=Q2'Q1'I'+Q2'PBTPHTC15+Q2Q1'I+Q2Q1I'+Q1'I'PBT'+Q1'I'C255
+Q1'I'PHT+Q2'Q1'PBTC15
Comme la vitesse n'est pas critique, il est possible de factoriser quelque peu certaines expressions.
J2=Q1'Q0'I'(PHT+PBT)+PBT'I(Q0C15+Q1)+Q1Q0(PBT'+C15)
K2=Q0I'(PBTPHT'C255+Q1)
J1=Q2'Q0'I'(PBT+PHT)+Q2Q0'I(PBT'+PHT')+Q2Q0I'(PHT+PBT')+Q2'Q0IC15
J0=Q1'(Q2'I+Q2I')+(IPBT')+Q2Q1I+Q1'IPHT'+Q2'IC255
K0=Q2'Q1'(I'+PBTC15)+Q2'PBTPHTC15+Q1'I'(PBT'+C255+PHT)+Q2(Q1'I+Q1I')
J'ai refait deux fois tous les calculs, je pense ne pas m'être trompé. Or une simulation du circuit ne fonctionne pas comme attendue. S'il commande aux différentes tensions jusqu'à l'allumage complet, basse et haute tensions, il indique une erreur lors de l'extinction. J'ai eu un peu de mal à comprendre mon erreur puisqu'elle ne résidait pas dans la réduction des quines mais dans une hypothèse hasardeuse. Bêtement, j'avais considéré que les basse et haute tensions avaient un temps de descente nul !
Il est donc nécessaire de rajouter une temporisation lors de l'extinction des différentes tensions avant de tester les absences de ces tensions.
Derniers raffinements de l'automate
Deprecated: Creation of dynamic property Item::$cache_has_content_parts is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 4911
Deprecated: Creation of dynamic property Item::$renderers_validated is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 11107
Deprecated: Creation of dynamic property Item::$pages is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 2412
Deprecated: Creation of dynamic property ItemSettings::$count_col_key_names is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/settings/model/_abstractsettings.class.php on line 121
Il manque à l'automate un dernier raffinement consistant en une transition allant de l'état 000 (repos) vers l'état 110 (défaut appareil éteint). En effet, si une tension de chauffage ou une haute tension apparaît dans le circuit commandé, l'alimentation est en panne et il convient de le signaler. Le nouveau diagramme des états devient alors :
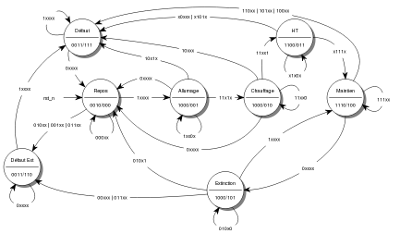
Fig. 1 : nouveau diagramme d'états (le même en grand)
Cette nouvelle transition ne change rien aux équations des sorties décrites plus tôt. En revanche, la table des transitions devient :
| Entrées | Sorties | |||||||||||||||
| Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q'2 | Q'1 | Q'0 | J2 | K2 | J1 | K1 | J0 | K0 |
| X | X | X | X | X | ||||||||||||
| 1 | X | X | 1 | 1 | 1 | X | 1 | X | X | |||||||
| 1 | X | X | 1 | 1 | 1 | X | 1 | X | X | |||||||
| 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | X | ||||||
| 1 | X | X | X | X | 1 | X | X | 1 | X | |||||||
| 1 | X | X | X | X | X | X | X | 1 | ||||||||
| 1 | 1 | X | X | X | 1 | X | X | X | ||||||||
| 1 | 1 | X | 1 | X | 1 | 1 | 1 | 1 | X | 1 | X | X | ||||
| 1 | 1 | 1 | X | 1 | X | 1 | X | 1 | X | X | 1 | |||||
| 1 | X | X | X | X | X | X | 1 | X | ||||||||
| 1 | 1 | X | X | X | 1 | 1 | 1 | 1 | X | X | 1 | X | ||||
| 1 | 1 | 1 | X | X | 1 | X | X | X | ||||||||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | X | 1 | X | |||||
| 1 | 1 | X | X | X | X | 1 | 1 | 1 | 1 | X | X | X | ||||
| 1 | 1 | X | 1 | 1 | X | 1 | 1 | 1 | 1 | X | X | X | ||||
| 1 | 1 | X | 1 | X | X | 1 | 1 | X | X | X | ||||||
| 1 | 1 | X | 1 | 1 | 1 | X | 1 | 1 | X | X | 1 | X | 1 | |||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | ||||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | ||||
| 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | |||||
| 1 | 1 | 1 | 1 | X | X | 1 | X | X | X | |||||||
| 1 | X | X | X | X | 1 | 1 | X | X | 1 | X | ||||||
| 1 | 1 | 1 | X | X | X | X | 1 | X | X | X | 1 | |||||
| 1 | 1 | 1 | X | 1 | X | 1 | X | X | 1 | |||||||
| 1 | 1 | 1 | X | 1 | 1 | X | X | X | ||||||||
| 1 | 1 | X | X | X | 1 | 1 | X | 1 | X | X | 1 | |||||
| 1 | 1 | 1 | 1 | X | X | 1 | 1 | X | 1 | X | X | 1 | ||||
| 1 | 1 | X | X | X | X | 1 | 1 | X | X | X | ||||||
| 1 | 1 | 1 | X | X | X | X | 1 | 1 | 1 | X | X | 1 | X | |||
| 1 | 1 | 1 | 1 | X | X | X | X | 1 | 1 | 1 | X | X | X | |||
| 1 | 1 | 1 | X | X | X | X | X | 1 | X | 1 | X | 1 | ||||
Tab. 1 : nouvelle table des transitions
Nouvelles transitions
Deprecated: Creation of dynamic property Item::$cache_has_content_parts is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 4911
Deprecated: Creation of dynamic property Item::$renderers_validated is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 11107
Deprecated: Creation of dynamic property Item::$pages is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/items/model/_item.class.php on line 2412
Deprecated: Creation of dynamic property ItemSettings::$count_col_key_names is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/settings/model/_abstractsettings.class.php on line 121
En gardant les mêmes notations qu'à l'article transitions, la nouvelle table de vérité est la suivante :
| Entrées | Sorties | |||||||||||||||
| Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q'2 | Q'1 | Q'0 | J2 | K2 | J1 | K1 | J0 | K0 |
| X | X | X | X | X | X | X | ||||||||||
| 1 | X | X | X | X | 1 | X | X | 1 | X | |||||||
| 1 | X | X | X | X | 0 | X | X | X | 1 | |||||||
| 1 | 1 | X | X | X | 1 | X | X | X | ||||||||
| 1 | 1 | X | 1 | X | 1 | 1 | 1 | 1 | X | 1 | X | X | ||||
| 1 | 1 | 1 | X | 1 | X | 1 | X | 1 | X | X | 1 | |||||
| 1 | X | X | X | X | 0 | X | X | 1 | X | |||||||
| 1 | 1 | X | X | X | 1 | 1 | 1 | 1 | X | X | 1 | X | ||||
| 1 | 1 | 1 | X | X | 1 | X | X | X | ||||||||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | X | 1 | X | |||||
| 1 | 1 | X | X | X | X | 1 | 1 | 1 | 1 | X | X | X | ||||
| 1 | 1 | X | 1 | 1 | X | 1 | 1 | 1 | 1 | X | X | X | ||||
| 1 | 1 | X | 1 | X | X | 1 | 1 | X | X | X | ||||||
| 1 | 1 | X | 1 | 1 | 1 | X | 1 | 1 | X | X | 1 | X | 1 | |||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | ||||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | ||||
| 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | |||||
| 1 | 1 | 1 | 1 | X | X | 1 | X | X | X | |||||||
| 1 | X | X | X | X | 1 | 1 | X | X | 1 | X | ||||||
| 1 | 1 | 1 | X | X | X | X | 1 | X | X | X | 1 | |||||
| 1 | 1 | 1 | X | 1 | X | 1 | X | X | 1 | |||||||
| 1 | 1 | 1 | X | 1 | 1 | X | X | X | ||||||||
| 1 | 1 | X | X | X | 1 | 1 | X | 1 | X | X | 1 | |||||
| 1 | 1 | 1 | 1 | X | X | 1 | 1 | X | 1 | X | X | 1 | ||||
| 1 | 1 | X | X | X | X | 1 | 1 | X | X | X | ||||||
| 1 | 1 | 1 | X | X | X | X | 1 | 1 | 1 | X | X | 1 | X | |||
| 1 | 1 | 1 | 1 | X | X | X | X | 1 | 1 | 1 | X | X | X | |||
| 1 | 1 | 1 | X | X | X | X | X | 1 | X | 1 | X | 1 | ||||
Tab. 1 : table de vérité du nouvel automate
Contrairement à la première table de vérité, les entrées J et K des bascules utilisent maintenant des états indifférents notés « X » qui devraient simplifier d'autant la synthèse du circuit logique.
Deprecated: preg_split(): Passing null to parameter #3 ($limit) of type int is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/_param.funcs.php on line 2201
Deprecated: preg_split(): Passing null to parameter #3 ($limit) of type int is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/_param.funcs.php on line 2201
Deprecated: preg_split(): Passing null to parameter #3 ($limit) of type int is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/_param.funcs.php on line 2201
Deprecated: preg_split(): Passing null to parameter #3 ($limit) of type int is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/_param.funcs.php on line 2201
Deprecated: preg_split(): Passing null to parameter #3 ($limit) of type int is deprecated in /export/home/bertrand/web/blog/b2evolution/blogs/inc/_core/_param.funcs.php on line 2201
<< 1 2 3 4 5 >>