Catégorie: "Schémas"
Bonne pour le service
La machine à états finis est maintenant bonne pour le service. Rien n'a été laissé au hasard.
Les équations des transitions sont les suivantes :
j0=q3'(I'(q2 xor q1)+I(PBT'+q2'(C255+q1')+q1PHT+q2PHT'))+q3q2'q1I
k0=q3((q2 xnor q1)+q1'PBT')+q2'PBTC15(q1'IPHT'+q3'q1PHT)
+q2I'(PBT'+q3'PHT+q1)
j1=q2'q0'I'(PHT+q3'PBT)+q3'q0I(PHT+C15)+q2PBT'(q0+I)
+q3q0'(PHT+PBTC15+q2)+q3'q2(q0PHT+IPHT')
k1=q3'(q2'(q0'I'+q0PBTPHTC15)+q2q0I')
j2=q1'q0'I'(PHT+q3'PBT)+q3'q0I(PBT'C15+q1'PHT)+q3q0'(PHT+q1+PBTC15)
+q3'q1(q0(C15+PBT')+IPBT')+q1q0'IPHT
k2=q3'q1'q0(I+PBTPHT'C255)+q1(q3+q0I')+q3q0'
j3=q0'I'(q2 xor q1)+q1'q0(I'(q2'+PBTPHT'C255)+q2I)
k3=q2'q0'(PHT+C15)+q2'q1+q2q1'q0(PBT'+C15)
Et le schéma complet devient :

Fig. 1 : la même chose en grand
Avec une horloge à 8 Hz, les tensions de chauffage sont présentes 64 s avant l'application de la haute tension. Lorsque la haute tension est coupée volontairement, les tensions de chauffage restent actives durant 64 s de plus. Les défauts d'une partie des alimentations provoquent une mise en sécurité du système.
La question est maintenant de savoir si j'implante la logique combinatoire dans une mémoire à diodes (512 mots de 5 bits, donc 2048 bits) ou en arithmétique pure.
Facile, non ?
Derniers raffinements
Je vois que personne n'a vu l'erreur signalée dans le dernier article. Le problème était simple, il fallait réinitialiser le compteur lors de la transition extinction vers HT. En effet, l'état extinction impose la présence de la basse tension, mais la haute tension est coupée. Lorsque cette haute tension est rallumée, son temps de montée n'est pas nul. Il faut donc passer par l'état HT qui ne vérifie pas la présence de la haute tension avant de passer en défaut ou en maintien. Or la transition depuis extinction vers HT se fait avec un compteur dans un état indéfini alors que l'arrivée à l'état HT suppose un compteur nul.
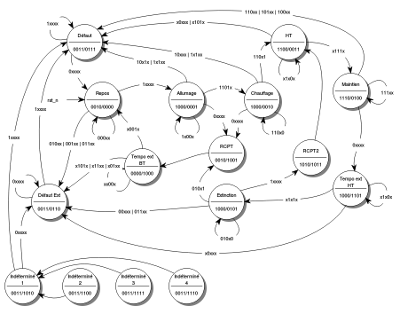
Fig. 1 : la même chose en grand
Les quatre états au bas du schéma sont des états normalement inaccessibles. Ils ont été rajoutés pour que tous les états soient déterminés et que le système passe en protection en cas de présence d'un état indéterminé.
Les nouvelles sorties de la machine sont maintenant :
| B | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | ||
| 11 | 1 | |||
| 10 | 1 | |||
Tab. 1 : allumage de la basse tension
B=Q3'(Q2'(Q0+Q1)+Q2Q1')+Q0(Q1 xor Q2)
| H | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | |||
| 11 | ||||
| 10 | ||||
Tab. 2 : allumage de la haute tension
H=Q3'(Q2Q1'Q0'+Q2'Q1Q0)
| R | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | 1 | 1 | |
| 11 | 1 | 1 | 1 | |
| 10 | 1 | 1 | 1 | |
Tab. 3 : blocage du compteur à zéro
R=Q1(Q2+Q3)+Q3'Q1'Q0'+Q3(Q2 xor Q0)
| E | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | ||||
| 01 | 1 | 1 | ||
| 11 | 1 | 1 | 1 | |
| 10 | 1 | |||
Tab. 4 : indicateur d'erreur
E=Q2Q1+Q3Q0'(Q2+Q1)
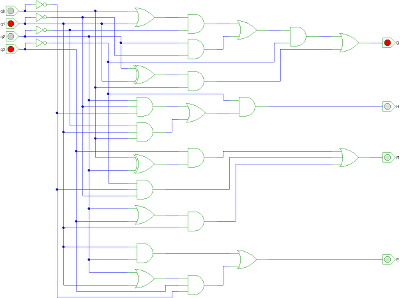
Fig. 2 : circuit de sortie de la machine (en grand)
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | 0 | 0 | 0 | 1 | X | X | X | X | ||||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | ||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 0 | 0 | 1 | 0 | X | X | X | X | ||||||
| 0 | 0 | 1 | 0 | 1 | X | 1 | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 1 | 0 | 1 | 1 | 1 | X | X | 1 | 1 | X | X | 0 |
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
| 1 | 0 | 1 | 1 | X | X | X | X | X | 0 | 0 | 1 | 1 | X | 1 | 0 | X | X | 0 | X | 0 |
| 1 | 0 | 1 | 0 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | X | 0 | 0 | X |
| 1 | 0 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | 1 | X | X | 0 | 1 | X |
| 1 | 1 | 0 | 0 | X | X | X | X | X | 1 | 0 | 1 | 0 | X | 0 | X | 1 | 1 | X | 0 | X |
| 1 | 1 | 1 | 1 | X | X | X | X | X | 1 | 0 | 1 | 0 | X | 0 | X | 1 | X | 0 | X | 1 |
| 1 | 1 | 1 | 0 | X | X | X | X | X | 1 | 0 | 1 | 0 | X | 0 | X | 1 | X | 0 | 0 | X |
Tab. 5 : transitions de l'automate
La réduction des quines et le schéma de câblage suivront au prochain épisode. Après tout, nous sommes dimanche.
Un pas de plus vers l'automatisation
Pour automatiser la réductions des quines, le programme présenté il y a quelques articles est modifié pour générer automatiquement les diverses équations réduites directement du tableau des transitions. La procédure se fait grâce à un premier programme qui transforme le tableau des transitions en autant de fichiers qu'il y a de commandes de bascules :
#!/usr/local/bin/rpl -csp
/*
* Format du fichier d'entrée :
* abcdefghia'b'c'd'j3k3j2k2j1k1j0k0
*/
TRANSITIONS
<<
{ "length*(1)" }
{ { "name" "transitions.global" } "sequential" "old"
"readonly" "flow" }
open format
0
-> F_IN NB_LIGNES
<<
while
F_IN "end of file" inquire not
repeat
""
do
F_IN read 1 get
until
if
dup "\n" same
F_IN "end of file" inquire or
then
drop true
else
+
false
end
end
if
dup "" same not
then
'NB_LIGNES' incr
else
drop
end
end
F_IN close
NB_LIGNES ->table
>>
14
-> L I
<<
{ "j3" "k3" "j2" "k2" "j1" "k1" "j0" "k0" }
forall E
{ "length*(*)" }
"name" "transitions." E +
if
dup "existence" inquire
then
{ "sequential" "replace" "readwrite" "flow" }
else
{ "sequential" "new" "readwrite" "flow" }
end
rot rot 2 ->list 1 ->list swap +
open format
-> FICHIER
<<
1 L size for K
L K 1 ->list get I dup sub
-> F
<<
if
F "0" same not
then
if
F "X" same
then
"*"
else
""
end
L K 1 ->list get 1 9 sub + "\n" +
1 ->list
FICHIER write
end
>>
next
FICHIER close
>>
'I' incr
next
>>
>>
Cette première étape est suivie par une seconde qui transforme l'écriture réduite des états en un fichier compréhensible par qmc-cli :
#!/usr/local/bin/rpl -csp
/*
* Format du fichier d'entrée :
* 010X00X
* *1111111
* *X000X01
*
* Le X correspond à une valeur indifférente. Les entiers binaires
* spécifiés doivent donner une combinaison vraie. Les lignes commençant par
* une étoile indiquent un résultat indifférent.
*/
PRINCIPAL
<<
{ "j0" "k0" "j1" "k1" "j2" "k2" "j3" "k3" }
forall I
I TRANSITIONS
next
>>
TRANSITIONS
<<
-> E
<<
{ "length*(1)" }
"name" "transitions." E + 2 ->list 1 ->list
{ "sequential" "old" "readonly" "flow" } +
open format
0
-> F_IN NB_LIGNES
<<
while
F_IN "end of file" inquire not
repeat
""
do
F_IN read 1 get
until
if
dup "\n" same
F_IN "end of file" inquire or
then
drop true
else
+
false
end
end
if
dup "" same not
then
'NB_LIGNES' incr
else
drop
end
end
F_IN close
NB_LIGNES ->list
>>
1
-> LISTE I
<<
do
LISTE I get ucase
-> E
<<
if
E "X" pos dup
then
// Il y a au moins un X
-> P
<<
{ "0" "1" } forall J
if
P 1 same
then
J E 2 over size sub +
elseif
P E size same
then
E 1 over size 1 - sub J +
else
E 1 P decr sub J +
E P incr E size sub +
end
next
LISTE swap I swap put swap
1 ->list + 'LISTE' sto
>>
else
// Pas de X, on passe au suivant
drop
'I' incr
end
>>
until
LISTE size I same
end
LISTE l->t << < >> sort
{ "length*(*)" }
"name" E ".in" +
if
dup "existence" inquire
then
{ "sequential" "replace" "flow" }
else
{ "sequential" "new" "flow" }
end
rot rot 2 ->list 1 ->list swap +
open format
-> F_OUT
<<
forall I
if
I "*" pos
then
"x" "# " I 2 over size sub + "b" + str->
b->r ->str +
else
"# " I + "b" + str-> b->r ->str
end
->str "\n" + 1 ->list F_OUT write
next
F_OUT close
>>
>>
>>
>>
À la fin de la procédure, les huit fichiers j0.in, j1.in, j2.in, j3.in, k0.in, k1.in, k2.in et k3.in sont créés. Reste à les faire passer dans la moulinette qmc-cli pour obtenir la réduction des quines.
Après réduction, les équations deviennent :
j0=q3'q2'((q1 xor i) + iC255)+q3'q2(q1'i'+iPHT)+q3'i(PBT'+q1PHT)
k0=q2'PBTC15(q1'iPHT'+q3'q1PHT)+q3'q2i'(q1+PHT)+q3q1'(q2'+q0PBT')
+q3'q2i'PBT'
j1=q3'q2'q0'i'(PBT+PHT)+q3'q0i(PHT+C15)+q3'q2(i(PBT'+PHT')+q0PHT)
+q3q2'q1'q0'(PHT+PBTC15)+q2q1'q0PBT'
k1=q3'q2'(q1'i'+q0PBTPHTC15)+q3'q2q0i'
j2=q3'q1'(q0'i'(PBT+PHT)+q0iPHT)+q3'q1(i(PBT'+qo'PHT)
+q0(PBT'+C15))+q3q2'q1'q0'(PHT+PBTC15)+q3'q0iPBT'C15
k2=q3'q0(q1'(i+PBTPHT'C255)+q1i')
j3=q3'q0'i'(q1 xor q2)+q1'i'(q3'q2PBTPHT'C255+q2'q0)
k3=q2'q1'q0'(PHT+C15)+q2q1'q0(PBT'+C15)
Le schéma du circuit de contrôle des alimentations devient alors :
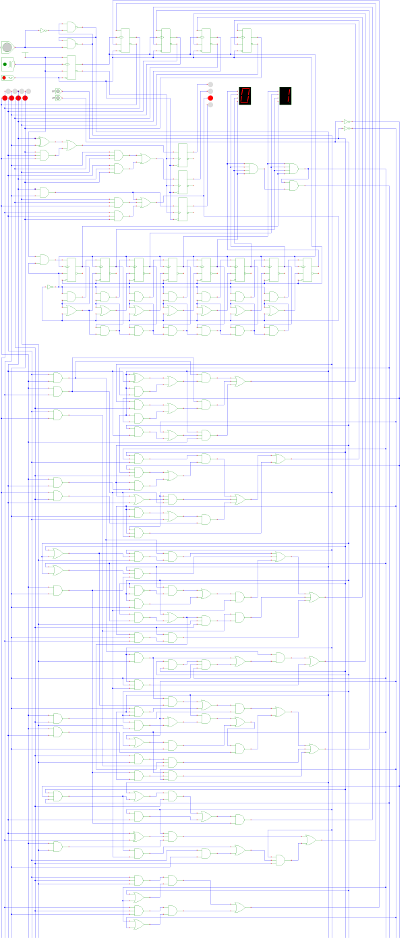
Fig. 1 : schéma de la machine à états (le même en grand)
J'ai pu tester ce circuit dans tous les sens. Il donne presque entièrement satisfaction. Tous les défauts sont bien détectés, les temporisations sont correctes pour les phases d'allumage et d'extinction. Ami lecteur, sauras-tu corriger ce circuit pour qu'il soit parfait ?
Automate, suite
Comme il faut toujours remettre son ouvrage sur le travail, voici la dernière version de l'automate à états finis gérant l'alimentation.
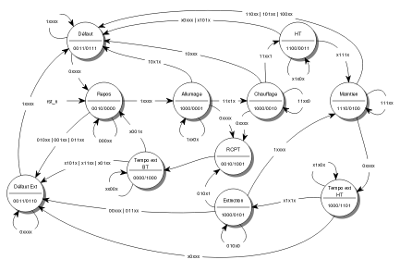
Fig. 1 : dernière version de l'automate (la même chose en grand)
J'espère cette fois-ci n'avoir rien oublié. Ce nouvel automate comporte onze états, donc nécessite quatre bascules au lieu de trois. Il faut donc réétudier les sorties du circuit à l'aide de nouveaux tableaux de Karnaugh.
| B | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | 1 | 1 | |
| 01 | 1 | 1 | ||
| 11 | X | 1 | X | X |
| 10 | X | X | ||
Tab. 1 : allumage de la basse tension
B=Q1'Q2+Q0Q2'Q3'+Q1Q2'
| H | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | |||
| 11 | X | X | X | |
| 10 | X | X | ||
Tab. 2 : allumage de la haute tension
H=Q2Q1'Q0'+Q2'Q1Q0
| R | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | 1 | |||
| 01 | 1 | 1 | 1 | |
| 11 | X | X | X | |
| 10 | 1 | X | X | |
Tab. 3 : blocage du compteur à zéro
R=Q3'Q1'Q0'+Q3Q2'Q0+Q2Q1
| E | Q1Q0 | |||
| Q3Q2 | 00 | 01 | 11 | 10 |
| 00 | ||||
| 01 | 1 | 1 | ||
| 11 | X | X | X | |
| 10 | X | X | ||
Tab. 4 : indicateur d'erreur
E=Q2Q1
Le schéma des quatre sorties devient alors :
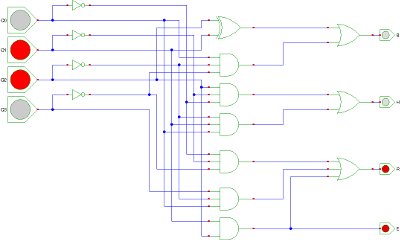
Fig. 1 : câblage des sorties (la même chose en grand)
Reste à écrire la table des transitions et à simplifier les quines.
| Entrées |
États futurs et |
|||||||||||||||||||
| Q3 | Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q3 | Q2 | Q1 | Q0 | J3 | K3 | J2 | K2 | J1 | K1 | J0 | K0 |
| 0 | 0 | 0 | 0 | X | X | 0 | 0 | 0 | 0 | X | X | X | X | |||||||
| 0 | 0 | 0 | 0 | 1 | X | X | X | X | 0 | 0 | 0 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | ||||
| 0 | 0 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | 1 | X | X | X | 0 | 0 | 0 | 1 | X | X | X | X | |||||
| 0 | 0 | 0 | 1 | 1 | X | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | 1 | X | X | |||
| 0 | 0 | 0 | 1 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | X | ||||
| 0 | 0 | 0 | 1 | 1 | 1 | X | 1 | X | 0 | 0 | 1 | 0 | X | X | 1 | X | X | 1 | ||
| 0 | 0 | 1 | 0 | X | X | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | 1 | X | ||
| 0 | 0 | 1 | 0 | 1 | 1 | X | X | 0 | 0 | 1 | 0 | X | X | X | X | |||||
| 0 | 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | 1 | X | |||
| 0 | 0 | 1 | 0 | 1 | 1 | X | X | 1 | 0 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 0 | 1 | 1 | X | 1 | X | X | 0 | 0 | 1 | 1 | X | X | X | X | |||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | 1 | X | 0 | 1 | 0 | 0 | X | 1 | X | X | 1 | X | 1 | |
| 0 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 0 | 1 | 1 | X | 1 | 1 | X | 0 | 1 | 1 | 1 | X | 1 | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 0 | 0 | X | X | X | X | ||||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | |||
| 0 | 1 | 0 | 0 | 1 | X | X | 0 | 1 | 1 | 1 | X | X | 1 | X | 1 | X | ||||
| 0 | 1 | 0 | 0 | X | X | X | X | 1 | 1 | 0 | 1 | 1 | X | X | X | 1 | X | |||
| 1 | 1 | 0 | 1 | X | 1 | X | X | 1 | 1 | 0 | 1 | X | X | X | X | |||||
| 1 | 1 | 0 | 1 | X | 1 | X | 1 | X | 0 | 1 | 0 | 1 | X | 1 | X | X | X | |||
| 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 0 | X | 1 | X | 1 | X | X | 1 | ||
| 0 | 1 | 0 | 1 | 1 | X | X | X | X | 0 | 1 | 0 | 0 | X | X | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 0 | 1 | 0 | 1 | X | X | X | X | |||||||
| 0 | 1 | 0 | 1 | X | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | ||||
| 0 | 1 | 0 | 1 | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | X | 1 | X | X | 1 | |||
| 0 | 1 | 0 | 1 | 1 | X | 1 | 1 | 0 | 0 | 1 | 1 | X | X | 1 | X | X | ||||
| 1 | 0 | 0 | 1 | X | X | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | 1 | |||
| 1 | 0 | 0 | 0 | X | X | X | 1 | 0 | 0 | 0 | X | X | X | X | ||||||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | |
| 1 | 0 | 0 | 0 | X | 1 | X | X | 0 | 1 | 1 | 0 | X | 1 | 1 | X | 1 | X | X | ||
| 1 | 0 | 0 | 0 | X | 1 | X | 0 | 0 | 0 | 0 | X | 1 | X | X | X | |||||
| 0 | 1 | 1 | 0 | X | X | X | X | 0 | 1 | 1 | 0 | X | X | X | X | |||||
| 0 | 1 | 1 | 0 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | 1 | X | |||
| 0 | 1 | 1 | 1 | X | X | X | X | 0 | 0 | 0 | 0 | X | X | 1 | X | 1 | X | 1 | ||
| 0 | 1 | 1 | 1 | 1 | X | X | X | X | 0 | 1 | 1 | 1 | X | X | X | X | ||||
Tab. 2 : transitions de l'automate
Derniers raffinements de l'automate
Il manque à l'automate un dernier raffinement consistant en une transition allant de l'état 000 (repos) vers l'état 110 (défaut appareil éteint). En effet, si une tension de chauffage ou une haute tension apparaît dans le circuit commandé, l'alimentation est en panne et il convient de le signaler. Le nouveau diagramme des états devient alors :
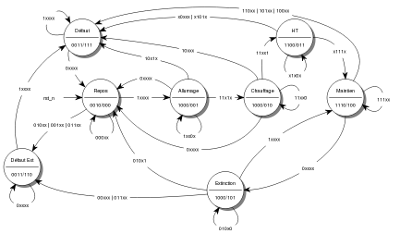
Fig. 1 : nouveau diagramme d'états (le même en grand)
Cette nouvelle transition ne change rien aux équations des sorties décrites plus tôt. En revanche, la table des transitions devient :
| Entrées | Sorties | |||||||||||||||
| Q2 | Q1 | Q0 | I | PBT | PHT | C15 | C255 | Q'2 | Q'1 | Q'0 | J2 | K2 | J1 | K1 | J0 | K0 |
| X | X | X | X | X | ||||||||||||
| 1 | X | X | 1 | 1 | 1 | X | 1 | X | X | |||||||
| 1 | X | X | 1 | 1 | 1 | X | 1 | X | X | |||||||
| 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | X | ||||||
| 1 | X | X | X | X | 1 | X | X | 1 | X | |||||||
| 1 | X | X | X | X | X | X | X | 1 | ||||||||
| 1 | 1 | X | X | X | 1 | X | X | X | ||||||||
| 1 | 1 | X | 1 | X | 1 | 1 | 1 | 1 | X | 1 | X | X | ||||
| 1 | 1 | 1 | X | 1 | X | 1 | X | 1 | X | X | 1 | |||||
| 1 | X | X | X | X | X | X | 1 | X | ||||||||
| 1 | 1 | X | X | X | 1 | 1 | 1 | 1 | X | X | 1 | X | ||||
| 1 | 1 | 1 | X | X | 1 | X | X | X | ||||||||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | X | 1 | X | |||||
| 1 | 1 | X | X | X | X | 1 | 1 | 1 | 1 | X | X | X | ||||
| 1 | 1 | X | 1 | 1 | X | 1 | 1 | 1 | 1 | X | X | X | ||||
| 1 | 1 | X | 1 | X | X | 1 | 1 | X | X | X | ||||||
| 1 | 1 | X | 1 | 1 | 1 | X | 1 | 1 | X | X | 1 | X | 1 | |||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | ||||
| 1 | 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | ||||
| 1 | 1 | X | X | 1 | 1 | 1 | X | 1 | X | 1 | X | |||||
| 1 | 1 | 1 | 1 | X | X | 1 | X | X | X | |||||||
| 1 | X | X | X | X | 1 | 1 | X | X | 1 | X | ||||||
| 1 | 1 | 1 | X | X | X | X | 1 | X | X | X | 1 | |||||
| 1 | 1 | 1 | X | 1 | X | 1 | X | X | 1 | |||||||
| 1 | 1 | 1 | X | 1 | 1 | X | X | X | ||||||||
| 1 | 1 | X | X | X | 1 | 1 | X | 1 | X | X | 1 | |||||
| 1 | 1 | 1 | 1 | X | X | 1 | 1 | X | 1 | X | X | 1 | ||||
| 1 | 1 | X | X | X | X | 1 | 1 | X | X | X | ||||||
| 1 | 1 | 1 | X | X | X | X | 1 | 1 | 1 | X | X | 1 | X | |||
| 1 | 1 | 1 | 1 | X | X | X | X | 1 | 1 | 1 | X | X | X | |||
| 1 | 1 | 1 | X | X | X | X | X | 1 | X | 1 | X | 1 | ||||
Tab. 1 : nouvelle table des transitions